La volta scorsa ho parlato delle comunicazioni di progetto e dei processi fondamentali per gestirle. Processi che da soli non bastano, perché qualsiasi interazione in un progetto si basa sull’insieme di capacità relazionali e di intelligenza emotiva, i cosiddetti soft skill, delle persone che vi prendono parte.
Tuttavia, seppure importanti, nemmeno spiccate dosi di soft skill danno garanzie assolute se i flussi di trasporto delle informazioni sono “disegnati” male. Per questo, affronto nuovamente il tema delle comunicazioni di progetto. Stavolta però da una prospettiva diversa, più ingegneristico-matematica, con l’obiettivo di individuare, se mai ve ne sono, regole e schemi per disegnare reti di comunicazioni di progetto “efficaci ed efficienti”.
Gli stakeholder di progetto sono una “rete sociale” che ha bisogno di coordinarsi attraverso lo scambio di informazioni, per far sì che le varie attività siano svolte e gli obiettivi raggiunti. La teoria delle reti sociali ha suscitato la curiosità di molti scienziati di diverse discipline, dagli psicologi ai matematici.
Puoi rappresentare una rete sociale con un grafo, un oggetto potente e generale, costituito da un insieme di nodi collegati da archi. In questo caso i nodi sono gli stakeholder di progetto e gli archi i flussi di comunicazione tra questi.
Quali requisiti deve avere la tua rete di comunicazioni di progetto?
- Deve essere efficace, cioè tutti i nodi del grafo devono essere connessi (non devono esserci nodi isolati) e le informazioni devono raggiungere tutti coloro a cui devono arrivare.
- Deve essere efficiente rispetto alle perdite durante il trasporto, cioè l’informazione deve arrivare al destinatario col minor numero di passaggi possibile.
- Deve essere efficiente rispetto al numero di flussi di comunicazione da attivare, perché ogni canale di comunicazione ha un costo.
- Deve essere resiliente, cioè il trasporto dell’informazione ai soggetti interessati deve essere garantito anche se alcuni canali di comunicazione risultano temporaneamente non disponibili.
Quanti sono i possibili flussi di comunicazione tra N soggetti? Al massimo N * (N – 1) / 2 nella situazione in cui ciascuno sia direttamente connesso a tutti gli altri. Come il numero di brindisi che puoi fare tra N commensali.
Il problema è che il numero delle connessioni aumenta in modo quadratico al crescere dei soggetti che comunicano. Applicando la formula di prima, tra 50 stakeholder puoi avere fino a 1.225 canali di comunicazione. Se però raddoppi il numero di stakeholder portandolo a 100, il numero di flussi quadruplica, diventando 4.950.
Uno scenario con decine o anche un centinaio di stakeholder è la norma per progetti di dimensioni medio-grandi, quindi dovresti chiederti se e come sia possibile assicurare una rete di comunicazioni efficace attivando solo una frazione (e con quale criterio) di tutti i flussi possibili.
Per rendere più comprensibile quello che dirò tra poco devo introdurre alcune definizioni relative alle reti. Si tratta di caratteristiche matematicamente misurabili, ma ai fini del nostro “allenamento” è sufficiente solo una loro definizione qualitativa.
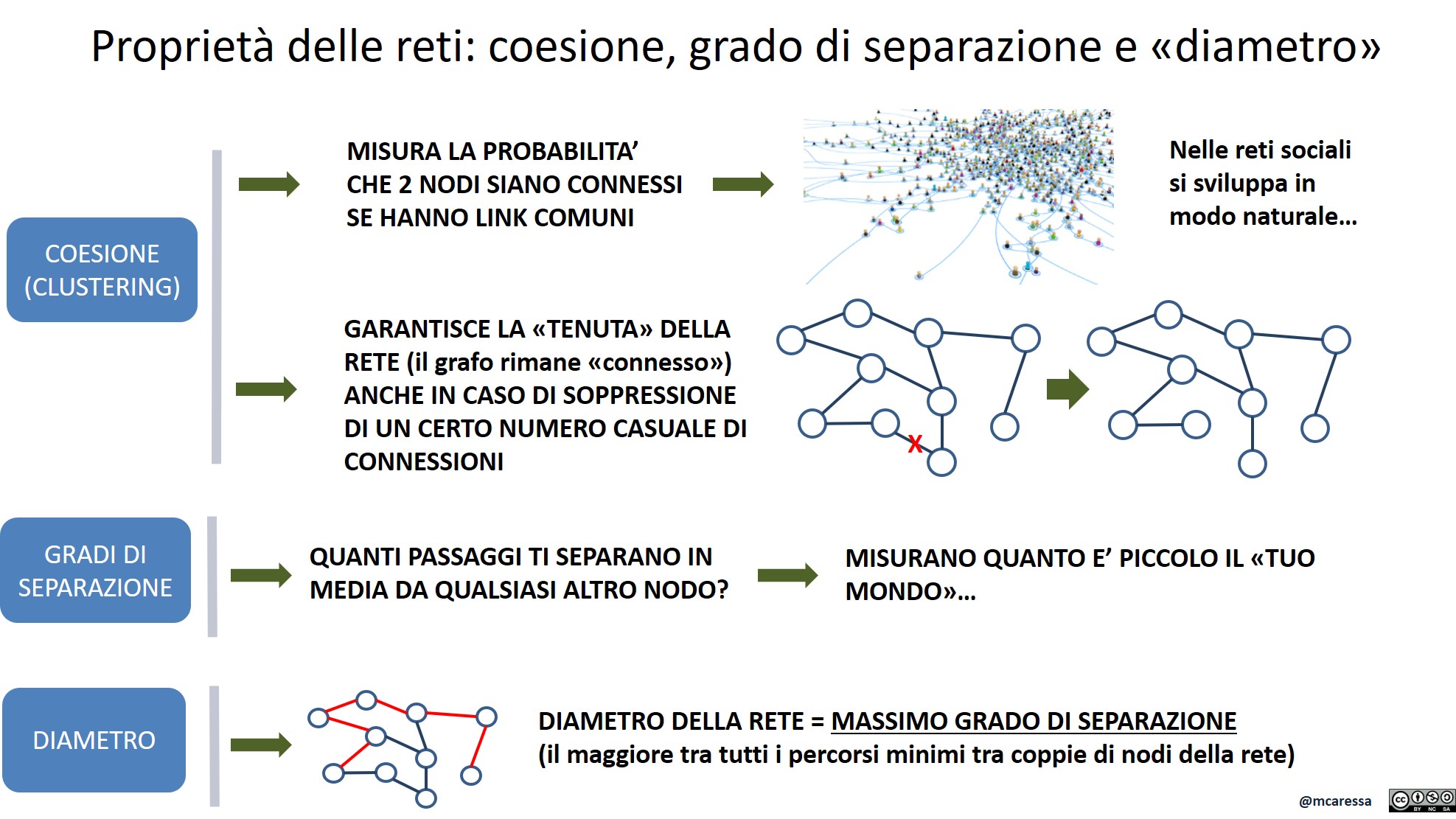
La coesione (clustering) misura la probabilità che 2 nodi siano connessi tra loro se hanno delle connessioni in comune. In poche parole, se io sono amico sia di Franco che di Luca è più probabile che Franco e Luca si conoscano tra loro. La coesione è anche ciò che rende una rete più “resiliente” ossia la capacità di rimanere “connessa” anche sopprimendo un certo numero di collegamenti.
I gradi di separazione sono i passaggi che devi fare per andare da un nodo all’altro e il “diametro della rete” ne rappresenta il valore massimo. Nel caso delle comunicazioni di progetto è il percorso più lungo che una informazione deve fare per raggiungere il destinatario.
Warm up
Che il mondo fosse davvero piccolo, al di là dei luoghi comuni, lo dimostrò Stanley Milgram nel 1967 con un esperimento di psicologia sociale, divenuto celebre come base per la cosiddetta teoria dei 6 gradi di separazione.
Per capire come si formassero le relazioni interpersonali, Milgram scrisse ad un campione casuale di residenti del Nebraska e del Kansas, chiedendo loro di inoltrare una lettera ad un suo amico agente di cambio di Boston. Tuttavia, invece di dar loro l’indirizzo li pregò di inoltrare la missiva ad un conoscente che avessero ritenuto socialmente affine al suo amico di Boston, dicendo di fare la stessa cosa a loro volta.
Invece di andare perdute, come ci si attendeva, la quasi totalità delle lettere non solo giunse a destinazione ma impiegò non più di 6 passaggi. La cosa sembrò inverosimile, non solo per la distanza geografica ma anche “sociale” tra dei cittadini qualunque del mid-west e un affermato professionista bostoniano. Con lo stesso criterio, tu sei separato da non più di 6 relazioni da qualsiasi altro essere umano sulla terra, inclusi Lebron James o Usain Bolt.
Qualche anno dopo due matematici, Duncan Watts e Steven Strogatz, cercavano di spiegare con la teoria dei grafi il comportamento di alcune colonie di lucciole tropicali, i cui migliaia di individui emettevano i loro segnali luminosi in perfetta sincronia, senza nessun agente esterno a dar loro il ritmo.
La coordinazione di un gruppo presuppone che i suoi individui possano comunicare e questo vale anche per le lucciole, così che che il comportamento di alcuni possa propagarsi ed influenzare anche gli altri. Watts e Strogatz simularono al computer 10.000 lucciole come nodi di un grafo, mettendo in connessione tutti con tutti. La formula che hai visto prima, con 10.000 nodi, dà 50 milioni di connessioni possibili. Nella simulazione, appena un nodo-lucciola avvistava una compagna lampeggiare si illuminava con un leggero anticipo rispetto a quanto avrebbe fatto per conto suo.
In queste condizioni, la sincronia tra tutte le lucciole veniva raggiunta quasi immediatamente ma lo scenario era poco realistico, perché in una vera colonia ciascun individuo non riesce a vedere tutte le altre migliaia di suoi simili, ma solo quelli più vicini. Watts e Strogatz modificarono il software di simulazione, cominciando a eliminare delle connessioni nel grafo in modo casuale e verificando che la sincronia veniva comunque raggiunta in breve tempo. Infine provarono uno schema diverso: eliminarono oltre il 99% delle 50 milioni di connessioni lasciando ciascun nodo-lucciola connesso solo con 4-5 vicini, tranne una piccolissima frazione, poche centinaia su 10.000, direttamente connessi a individui molto “lontani” nella rete. La sincronia continuava ad essere raggiunta in modo rapido!
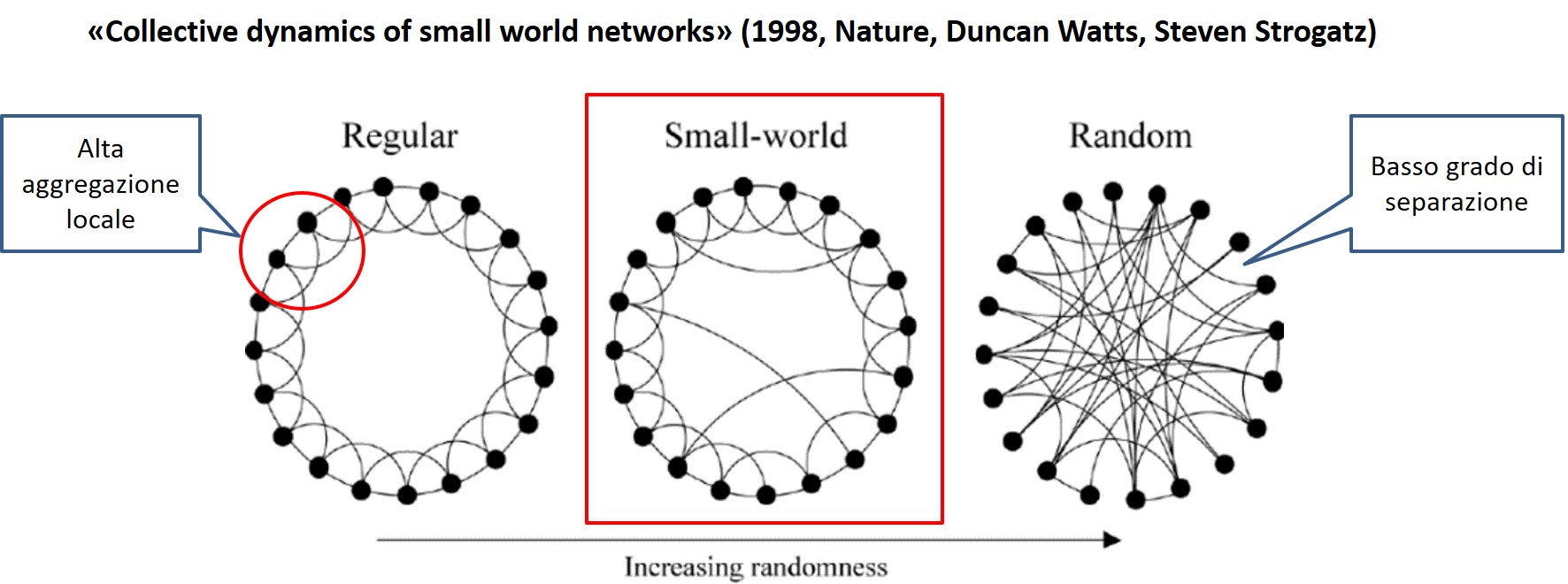
Sia nel caso dell’esperimento di Milgram che delle lucciole virtuali di Watts e Strogatz abbiamo una rete che manifesta delle proprietà cosiddette di “piccolo mondo” (small world network). Le lettere arrivano dal mid-west a Boston e le lucciole si sincronizzano perché in entrambi i casi tutti gli individui sono coesi localmente (ciascuno ha una cerchia ristretta di vicini) mentre pochi hanno delle connessioni di lunga gittata con individui molto lontani e sono proprio quei pochi a fare la differenza. Il risultato è una rete con un basso grado di separazione, dove le informazioni si propagano rapidamente (efficace) utilizzando solo una piccola frazione delle connessioni possibili (efficiente).
Esercizi
A questo punto sei pronto per sostituire ai corrispondenti di Milgram e alle lucciole di Watts e Strogatz gli stakeholder di progetto per provare a farli comunicare al meglio.
Esercizio N. 1, criteri per disegnare una generica rete di comunicazione tra stakeholder
Scenario 1: minimizzare il numero di connessioni. Immagina un progetto semplice con 12 stakeholder. Per disegnare la rete di comunicazioni risparmiando il più possibile sul numero di connessioni puoi definire uno schema come quello seguente, connettendo ogni nodo solo con i 2 nodi adiacenti. Ti bastano così 12 connessioni. Il numero minimo per collegare N nodi sarebbe N-1, cioè 11, mettendoli tutti in fila indiana, ma “chiudere la collana” ti consente di diminuire il percorso medio per andare da un nodo all’altro.
Il diametro della rete (max numero di passaggi per portare l’informazione) è pari a 6. Quindi risparmiando sul numero di connessioni abbiamo flussi di comunicazione in media con molti passaggi e maggiore perdita potenziale di informazione, oltre ad una bassa resilienza, perché se due collegamenti qualsiasi vengono meno la rete degenera in due gruppi distinti di stakeholder isolati. In definitiva, non si tratta di uno schema soddisfacente rispetto ai requisiti fissati in precedenza.

Scenario 2, minimizzare il grado di separazione. Sempre con i 12 stakeholder di prima, prova adesso a connettere tutti con tutti (N * (N-1) / 2 = 66 connessioni).
Il grado di separazione è pari a 1 per tutti gli stakeholder, quindi l’informazione arriva sempre e comunque con un solo passaggio e la rete può sopportare la soppressione casuale di diversi collegamenti prima che l’efficienza di trasporto dell’informazione degradi sensibilmente. Sembrerebbe che l’unico problema sia il costo dell’attivazione di tutte queste connessioni ma in realtà anche questo schema non è soddisfacente.
In una situazione reale, se tutti sono in grado di comunicare direttamente con tutti si genera una ridondanza e un sovraccarico che minano l’efficacia del trasporto di informazione. Un po’ come quando ti ritrovi delle email nella tua casella di posta solo perché qualcuno improvvidamente ha fatto una “reply all”.

Scenario 3, rete “piccolo mondo”: basso grado di separazione con poche connessioni. Puoi ottenere una rete “piccolo mondo” riprendendo quella minimale dello scenario 1 e aggiungendo solo 3 collegamenti trasversali. Al costo di 3 sole connessioni in più rispetto allo scenario minimo i gradi di separazione si dimezzano passando da 6 a 3, garantendo velocità ed efficienza di trasporto. Il clustering è più alto e con esso la resilienza della rete, senza ridondanza di flussi

Come devi eseguire questo esercizio? In realtà l’esercizio è costituito dal solo scenario 3. I primi 2 scenari servivano solo per far emergere dei criteri generali di progettazione della rete di comunicazioni, la cui definizione viene affrontata all’inizio del progetto. Se ricordi gli esercizi della volta scorsa, la versione finale della rete di comunicazioni diventa parte del Piano delle Comunicazioni, dove viene definito chi deve comunicare con chi (e con quale modalità). Questa analisi può naturalmente essere rivista anche in corso d’opera, ogni qualvolta vi siano modifiche agli stakeholder di progetto (es. aggiunta o rimozione di nodi dalla rete), determinando un conseguente aggiornamento del Piano.
Esercizio 2: individua gli “stakeholder hub”
Hai appena visto che le comunicazioni tra gli stakeholder di progetto disegnate come una rete “piccolo mondo” soddisfano mediamente bene tutti i requisiti fissati all’inizio (efficacia, efficienza, resilienza). Il carattere “piccolo mondo” della rete è dato dai pochi legami trasversali che mettono in comunicazione cluster di nodi locali, che fanno comportare i tuoi stakeholder come le lucciole di Watts e Strogatz. Ci sono però due tipi di rete piccolo mondo, in funzione di come sono distribuiti questi legami trasversali.
Se la loro distribuzione è casuale parliamo di “reti egualitarie” (con ovvio significato del termine). Se invece i collegamenti trasversali sono concentrati su pochi nodi “hub” parliamo di “reti aristocratiche” (dovendo trovare una descrizione evocativa di segno opposto).
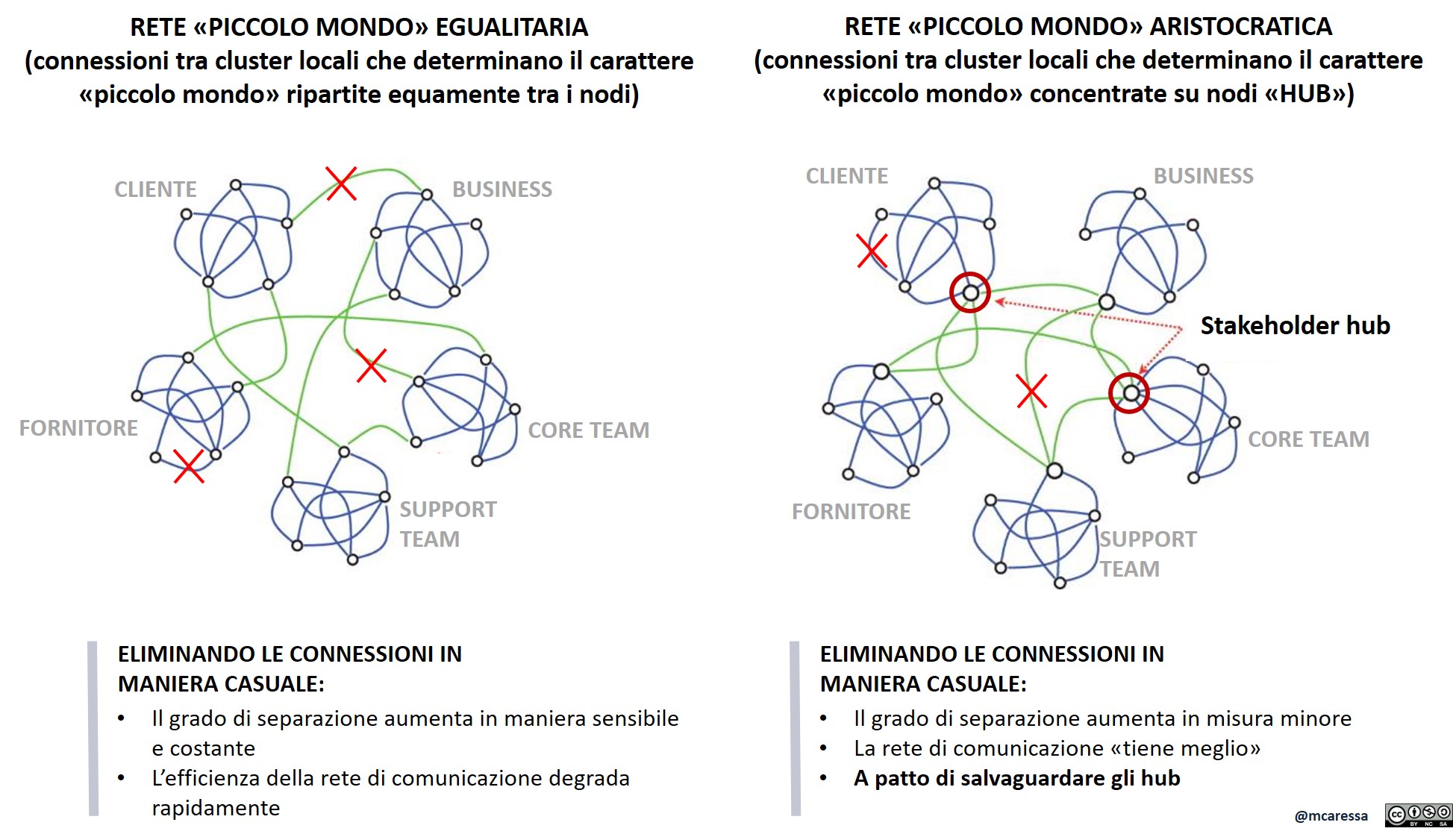
Ci sono in natura, o come opere dell’uomo, diversi esempi dell’una e dell’altra tipologia, ma per i tuoi scopi una rete di comunicazione tra stakeholder “aristocratica”, basata cioè sulla presenza di “hub”, è più adatta perché la sua resilienza degrada più lentamente se alcuni dei canali di comunicazione che predisponi non dovessero essere disponibili e se questa indisponibilità non sia “mirata” ma casuale. Non posso dimostrartelo qui, ci vorrebbe troppo tempo. Tieni comunque presente che la stessa Internet è una rete piccolo mondo di tipo “aristocratico”, quindi molto resiliente rispetto a guasti casuali anche importanti. Il discorso cambia se la perdita di collegamenti non è casuale ma dolosa. Un “black hat” (termine per indicare un hacker cattivo) che voglia creare il maggior disservizio possibile attaccherà I nodi hub.
Devi perciò individuare gli stakeholder hub del tuo progetto. Sono quelli attraverso i quali devono passare gran parte dei flussi di informazioni perché di solito sono anche quelli che prendono le decisioni. Per farlo puoi utilizzare il risultato della stakeholder analysis di cui ho parlato in una scheda di allenamento qualche mese fa e a cui ti rimando.
Come devi eseguire questo esercizio? Questo esercizio è il completamento del precedente e serve ad aggiustare in modo “fine” i canali di comunicazione tra gli stakeholder che avevi già individuato in prima istanza, in particolare quelli trasversali tra cluster locali che determinano il carattere “piccolo mondo” della rete, concentrandoli sugli hub.
Defaticamento e stretching
L’efficacia e l’efficienza delle comunicazioni di progetto non dipende soltanto dall’applicazione di processi e dal possesso di soft skill e di doti relazionali dei protagonisti, ma anche dalla struttura della rete di comunicazioni, disegnata come parte delle attività di attività di pianificazione delle comunicazioni di progetto per garantire che a ogni stakeholder arrivi la corretta informazione nel giusto momento.
Questa rete di comunicazioni può avere le caratteristiche di una “rete piccolo mondo”, che con pochi collegamenti determina un basso grado di separazione, cioè trasporto di informazioni veloce e con poche perdite. Tali caratteristiche sono una elevata coesione locale e pochi ma mirati collegamenti trasversali di “lunga gittata” che mettono in comunicazione rapidamente cluster locali di stakeholder altrimenti troppo distanti.
In particolare, concentrare questi canali di comunicazione trasversali su opportuni stakeholder “hub” permette alla rete di essere più resiliente, cioè di mantenere le sue caratteristiche di efficienza anche nel caso in cui alcuni collegamenti non fossero disponibili per motivi casuali (imprevisti, guasti o altre problematiche).
Non è un caso che una rete piccolo mondo sia un buon modello per le comunicazioni di progetto. Si tratta di una struttura ubiqua in natura quasi come la serie di Fibonacci. Hanno una struttura di “piccolo mondo” le reti neurali biologiche, le reti elettriche, le reti stradali, Interrnet, i link di un sito web, le colonie di lucciole tropicali e molte altre cose insospettabili.
D’altra parte, se Milgram riuscì a far arrivare quelle lettere al suo amico di Boston tramite sconosciuti del Kansas e del Nebraska in non più di 6 passaggi, con un po’ di allenamento e conoscendo i tuoi stakeholder dovresti essere in grado di fare anche meglio. In ogni caso, come direbbe Austin Kleon “Be nice. The world is a small town”.










Facebook Comments